Homework #7 Solutions


Reminder - you're going to need these webpages: http://www.continuummechanics.org/techforms/index.html to do this homework.... unless you prefer to use Matlab, Mathematica, etc.


  1. Figure out the deformation gradient at the center of the element below.




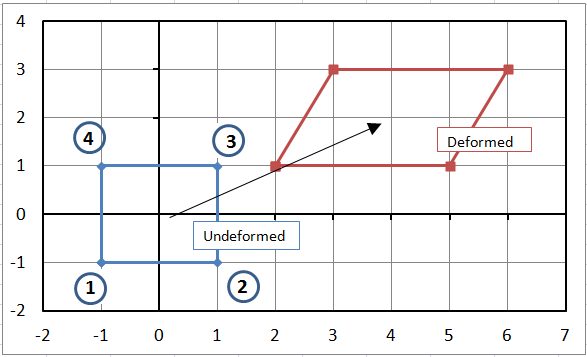
    2. The node displacements are

    \[ \begin{eqnarray} u_1 = 3 \qquad u_2 = 4 \qquad u_3 = 5 \qquad u_4 = 4 \\ v_1 = 2 \qquad v_2 = 2 \qquad v_3 = 2 \qquad v_4 = 2 \end{eqnarray} \]

    The deformation gradient components are

    \[ \begin{eqnarray} F_{11} & = & {1 \over 4} [-(1-Y)u_1 + (1-Y)u_2 + (1+Y)u_3 - (1+Y)u_4] + 1 \\ \\ & = & {1 \over 4} [-u_1 + u_2 + u_3 - u_4] + 1 \\ \\ \\ & = & 1.5 \\ \\ F_{12} & = & {1 \over 4} [-(1-X)u_1 - (1+X)u_2 + (1+X)u_3 + (1-X)u_4] \\ \\ & = & {1 \over 4} [-u_1 - u_2 + u_3 + u_4] \\ \\ \\ & = & 0.5 \\ \\ F_{21} & = & {1 \over 4} [-(1-Y)v_1 + (1-Y)v_2 + (1+Y)v_3 - (1+Y)v_4] \\ \\ & = & {1 \over 4} [-v_1 + v_2 + v_3 - v_4] \\ \\ \\ & = & 0.0 \\ \\ F_{22} & = & {1 \over 4} [-(1-X)v_1 - (1+X)v_2 + (1+X)v_3 + (1-X)v_4] + 1 \\ \\ & = & {1 \over 4} [-v_1 - v_2 + v_3 + v_4] + 1 \\ \\ \\ & = & 1.0 \end{eqnarray} \]

    \[ {\bf F} = \left[ \matrix{ 1.5 & 0.5 \\ 0.0 & 1.0 } \right] \]

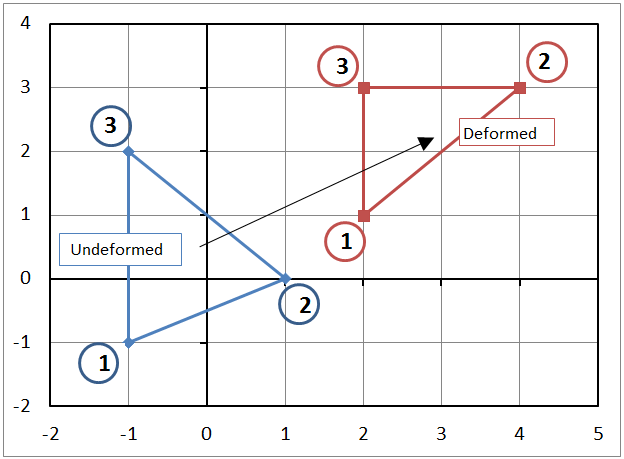
  2. Figure out the deformation gradient in this element.



    3. The undeformed node coordinates are

    \[ \begin{eqnarray} X_1 = -1 & \qquad X_2 = 1 & \qquad X_3 = -1 \\ \\ Y_1 = -1 & \qquad Y_2 = 0 & \qquad Y_3 = 2 \end{eqnarray} \]

    The node displacements are

    \[ \begin{eqnarray} u_1 = 3 & \qquad u_2 = 3 & \qquad u_3 = 3 \\ \\ v_1 = 2 & \qquad v_2 = 3 & \qquad v_3 = 1 \end{eqnarray} \]

    The partial derivatives are

    \[ \begin{eqnarray} \left[ \matrix{ {\partial u \over \partial X} & {\partial u \over \partial Y} \\ \\ {\partial v \over \partial X} & {\partial v \over \partial Y} } \right] & = & \left[ \matrix{ u_1 - u_3 & u_2 - u_3 \\ \\ v_1 - v_3 & v_2 - v_3 \\ } \right] \left[ \matrix{ X_1 - X_3 & X_2 - X_3 \\ \\ Y_1 - Y_3 & Y_2 - Y_3 \\ } \right]^{-1} \\ \\ \\ \\ & = & \left[ \matrix{ 0 & 0 \\ \\ 1 & 2 \\ } \right] \left[ \matrix{ \;\;\;0 & \;\;\;2\\ \\ -3 & -2 \\ } \right]^{-1} \\ \\ \\ \\ \\ \\ & = & \left[ \matrix{ 0 & 0 \\ \\ 1 & 2 \\ } \right] \left[ \matrix{ -0.333 & -0.333 \\ \\ \;\;\;0.500 & \;\;\;0.000 \\ } \right] \\ \\ \\ \\ \\ \\ & = & \left[ \matrix{ 0.000 & \;\;\;0.000 \\ \\ 0.667 & -0.333 \\ } \right] \end{eqnarray} \]

    And add \( {\bf I}\) to get \({\bf F}\).

    \[ {\bf F} = \left[ \matrix{ 1.000 & 0.000 \\ \\ 0.667 & 0.667 \\ } \right] \]



  3. How many degrees of rigid body rotation is this element experiencing?



    4. The polar decomposition can be applied to get


    \[ {\bf R} = \left[ \matrix{ 0.928 & -0.371 \\ \\ 0.371 & \;\;\;0.928 } \right] \qquad \qquad {\bf U} = \left[ \matrix{ 1.176 & 0.248 \\ \\ 0.248 & 0.619 } \right] \]
    So this element rotates

    \[ \theta \quad = \quad \text{Sin}^{-1}(0.371) \quad = \quad 21.8^\circ \]