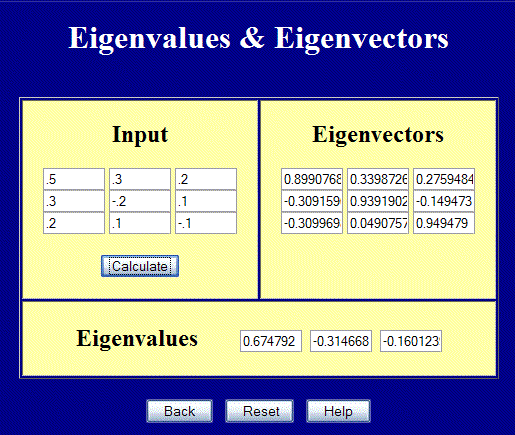
\[ {\bf E} = \left[ \matrix{ 0.10 & 0.60 & 0.00 \\ 0.60 & 0.00 & 0.00 \\ 0.00 & 0.00 & 0.00 } \right] \]
Start with the principal values. They are 0.652 and -0.552.

This confirms that one of the principal values in this Green strain tensor is indeed less than -0.50.
Since \({\bf E} = {1 \over 2}({\bf F}^T \cdot {\bf F} - {\bf I})\), then \(({\bf F}^T \cdot {\bf F} = 2{\bf E} + {\bf I})\). Doing this gives
\[ {\bf F}^T \cdot {\bf F} = \left[ \matrix{ 1.20 & 1.20 & 0.00 \\ 1.20 & 1.00 & 0.00 \\ 0.00 & 0.00 & 1.00 } \right] \]
We don't care about rotations, so just assume they're zero. This means that \({\bf F} = {\bf U}\) for this problem. So we are back to the usual polar decomposition problem of needing to find \({\bf U}\), given
\[ {\bf F}^T \cdot {\bf F} = {\bf U}^T \cdot {\bf U} = \left[ \matrix{ 1.20 & 1.20 & 0.00 \\ 1.20 & 1.00 & 0.00 \\ 0.00 & 0.00 & 1.00 } \right] \]
Taking the first step of solving for \({\bf U}\) by calculating the principal values of \({\bf U}^T \cdot {\bf U}\) gives
\[ ({\bf U}^T \cdot {\bf U})' = \left[ \matrix{ 2.304 & 0 & 0 \\ 0 & -0.104 & 0 \\ 0 & 0 & 1.00 } \right] \]
The next step would be to take the square root of the diagonal values, but this is impossible because the (2,2) slot is negative. This is critical because a negative principal value in \({\bf U}_{princ}\), (actually \({\bf U}^2_{princ}\)) means that the material has turned inside out!
\[ \begin{eqnarray} x & = & 0.530 X - 0.530 Y + 2 \\ \\ y & = & 0.884 X + 0.884 Y + 1 \end{eqnarray} \]
Do the following:
- Sketch the undeformed square, and also its deformed shape.
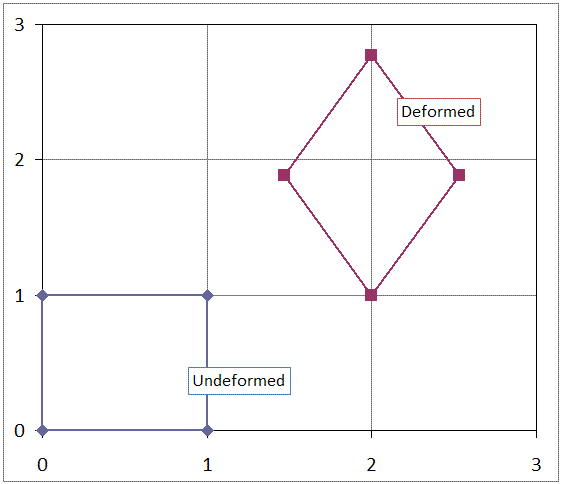
The deformation gradient is
\[ {\bf F} = \left[ \matrix{ 0.530 & -0.530 \\ 0.884 & \;\;\;0.884 } \right] \]
Calcuate the Green Strain...
\[ {\bf E} = {1 \over 2} \left( {\bf F}^T \! \cdot {\bf F} - {\bf I} \right) = \left[ \matrix{ 0.031 & 0.250 \\ 0.250 & 0.031 } \right] \]
The principal strains and \({\bf Q}\) matrix are
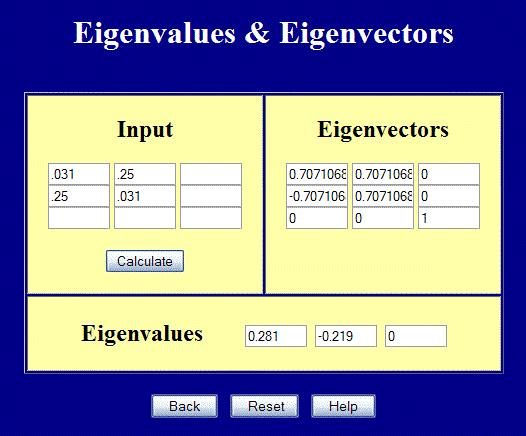
The principal orientation is
\[ \begin{eqnarray} \theta & = & \text{Sin}^{-1}(Q_{12}) \\ \\ & = & \text{Sin}^{-1}(0.7071) \\ \\ & = & 45^\circ \end{eqnarray} \]
which means it is 45° from the X-axis because it is based on the Green strain, which is "undeformed."
We need to know how much rigid body rotation is present because this needs to be added to the 45°: angle above to get the final deformed orienation. (This is the key insight here.)
So do a polar decomposition...

The rigid body rotation is
\[ \begin{eqnarray} \theta & = & \text{Sin}^{-1}(R_{21}) \\ \\ & = & \text{Sin}^{-1}(0.7071) \\ \\ & = & 45^\circ \end{eqnarray} \]
So the final orientation of the principal directions are 45° + 45° = 90°, and then another 90° from that for the second principal strain.
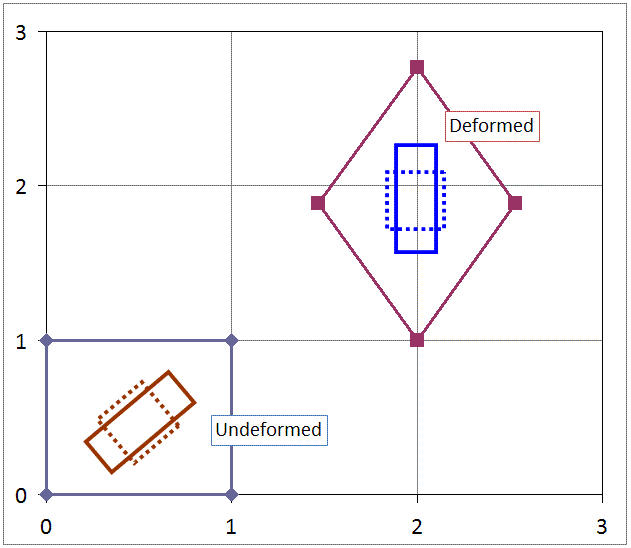
It is only when you add in the rigid body rotation to the Green strain principal directions.
Note - An \({\bf F} = {\bf V}\cdot{\bf R}\) polar decomposition also gives some insight into this problem. Doing so gives
\[ {\bf V} = \left[ \matrix{ 0.75 & 0.00 & \;\;0 \\ 0.00 & 1.25 & \;\;0 \\ 0 & 0 & \;\;1 } \right] \qquad {\bf R} = \left[ \matrix{ 0.7071 & -0.7071 & \;\;0 \\ 0.7071 & \;\;\;0.7071 & \;\;0 \\ 0 & 0 & \;\;1 } \right] \]
The \({\bf V}\) matrix shows that the X and Y directions are the principal directions because there are no shears present. This is consistent with the above conclusion that the principal directions are at 45° + 45° = 90° for the 1st principal direction, and then another 90° from that for the 2nd.