Introduction
This page presents the so-called infinitesimal strain definitions. This is a bit of a misnomer because as we will see in smallstrain.html, it is actually rotations that need to be small, not the strains themselves, in order to accurately use the small strain equations.Normal Strains
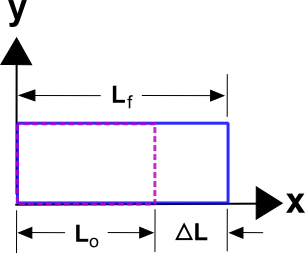
Normal in normal strain does not mean common, or usual strain. It means a direct length-changing stretch (or compression) of an object resulting from a normal stress. It is commonly defined as\[ \epsilon = {\Delta L \over L_o} \]
where the quantities are defined in the sketch. This is also known as Engineering Strain. Note that when \(\Delta L\) is small, then \(L_o\) will be so close to \(L_f\) that the specification of either in the denominator of \(\Delta L / L\) is unnecessary, in fact. This will be assumed to be the case throughout this page.
The definition arises from the fact that if a 1 m long rope is pulled and fails after it stretches 0.015 m, then we would expect a 10 m rope to stretch 0.15 m before it fails. In each case, the strain is \(\epsilon\) = 0.015, or 1.5%, and is a constant value independent of the rope's length, even though the \(\Delta L's\) are different values in the two cases. Likewise, the force required to stretch a rope by a given amount would be found to depend only on the strain in the rope. It is this foundational concept of strain that makes this definition a useful choice.
Shear Strains
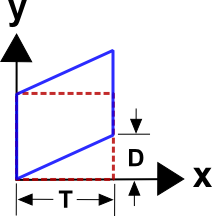
Shear strain is usually represented by \(\gamma\) and defined as\[ \gamma = {D \over T} \]
This is the shear-version of engineering strain. Note that this situation does include some rigid body rotation because the square tends to rotate counter-clockwise here, but we will ignore this complication for now.
Pure Shear Strains
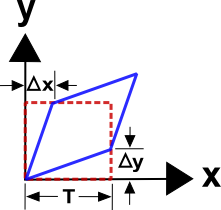
So a better, but slightly more complex definition of shear strain, is
\[ \gamma = { \Delta x + \Delta y \over T} \]
where it is assumed that the starting point is also a square. It should be noted that the two definitions lead to the same results when the displacements and strains are small. In other words
\[ \Delta x = \Delta y = { D \over 2} \qquad \text{(small strains)} \]
This permits one to think in terms of the first definition while using the second.
General Definitions
The above definitions are good in that they work for simple cases in which all the strain is one or the other (normal or shear). But as soon as the strain components are simultaneously present for \(\epsilon_x, \epsilon_y, \epsilon_z, \gamma_{xy}\), etc., things can become unmanageable. So a more general method of calculation is needed.The answer to this dilemma is... calculus. The approach is to define the various strains in terms of partial derivatives of the displacement field, \({\bf u({\bf X})}\), in such a way that the above definitions are preserved for the simple cases.
Normal Strains
The normal strains are defined as\[ \epsilon_x = {\partial \, u_x \over \partial X} \qquad \epsilon_y = {\partial \, u_y \over \partial Y} \qquad \epsilon_z = {\partial \, u_z \over \partial Z} \]
The simple case of uniaxial stretching can be described as
\[ x = \left( {X \over L_o} \right) L_f \]
and since \({\bf u} = {\bf x} - {\bf X}\), a little algebra can be applied to give
\[ u_x = \left( {X \over L_o} \right) \left( L_f - L_o \right) \]
So
\[ \epsilon_x \quad = \quad {\partial \, u_x \over \partial X} \quad = \quad {L_f - L_o \over L_o} \quad = \quad {\Delta L \over L_o} \]
which reproduces the "delta L over L" definition as desired.
Shear Strains
The equation for shear strain is\[ \gamma_{xy} = {\partial \, u_y \over \partial X} + {\partial \, u_x \over \partial Y} \]
The coordinate mapping equation for the shear example is
\[ \begin{eqnarray} x & = & X \\ y & = & Y + X D / T \end{eqnarray} \]
And the displacement field is
\[ \begin{eqnarray} u_x & = & 0 \\ u_y & = & X D / T \end{eqnarray} \]
The shear strain is
\[ \gamma_{xy} \quad = \quad {\partial \, u_y \over \partial X} + {\partial \, u_x \over \partial Y} \quad = \quad {\partial \, (X D / T) \over \partial X} + {\partial \, (0) \over \partial Y} \quad = \quad {D \over T} \]
This reproduces the desired result for this simple case: \(\gamma_{xy} = D / T\).
The symmetry of the equation also ensures that the computed shear value also satisfies the no-net-rotation criterion. The coordinate mapping equations for this example are
\[ \begin{eqnarray} x & = & X & + & Y \Delta x / T \\ y & = & Y & + & X \Delta y / T \end{eqnarray} \]
and they lead to
\[ \gamma_{xy} = {\Delta x + \Delta y \over T} \]
which again produces the desired result.
2-D Notation
Strain, like stress, is a tensor. And like stress, strain is a tensor simply because it obeys the standard coordinate transformation principles of tensors. It can be written in any of several different forms as follows. They are all identical.But since \(\gamma_{xy} = \gamma_{yx}\), all the tensors can also be written as
\[ \boldsymbol{\epsilon} = \left[ \matrix{ \epsilon_{11} & \epsilon_{12} \\ \epsilon_{12} & \epsilon_{22} } \right] = \left[ \matrix{ \epsilon_{xx} & \epsilon_{xy} \\ \epsilon_{xy} & \epsilon_{yy} } \right] = \left[ \matrix{ \epsilon_{xx} & \gamma_{xy}/2 \\ \gamma_{xy}/2 & \epsilon_{yy} } \right] \]
Setting \(\gamma_{xy} = \gamma_{yx}\) has the effect of making (requiring in fact) the strain tensors symmetric.
Tensor Shear Terms
VERY IMPORTANT: The shear terms here possess a property that is common across all strain definitions and is an endless source of confusion and mistakes. The shear terms in the strain tensor are one-half of the engineering shear strain values defined earlier as \(\gamma_{xy} = D / T\). This is acceptable and even necessary in order to correctly perform coordinate transformations on strain tensors. Nevertheless, tensorial shear terms are written as \(\epsilon_{ij}\) and are one-half of \(\gamma_{ij}\) such that\[ \gamma_{ij} = 2 \epsilon_{ij} \]
It is always, always, always the case that if \(\gamma_{xy} = D / T = 0.10\), then the strain tensor will contain
\[ \boldsymbol{\epsilon} = \left[ \matrix{ ... & 0.05 & ... \\ 0.05 & ... & ... \\ ... & ... & ... } \right] \]
Alternatively, if the strain tensor is
\[ \boldsymbol{\epsilon} = \left[ \matrix{ ... & 0.02 & ... \\ 0.02 & ... & ... \\ ... & ... & ... } \right] \]
then \(\gamma_{xy} = D / T = 0.04\).
3-D Notation
\[ \boldsymbol{\epsilon} = \left[ \matrix{ \epsilon_{11} & \epsilon_{12} & \epsilon_{13} \\ \epsilon_{21} & \epsilon_{22} & \epsilon_{23} \\ \epsilon_{31} & \epsilon_{32} & \epsilon_{33} } \right] = \left[ \matrix{ \epsilon_{xx} & \epsilon_{xy} & \epsilon_{xz} \\ \epsilon_{yx} & \epsilon_{yy} & \epsilon_{yz} \\ \epsilon_{zx} & \epsilon_{zy} & \epsilon_{zz} } \right] = \left[ \matrix{ \epsilon_{xx} & \gamma_{xy}/2 & \gamma_{xz}/2 \\ \gamma_{yx}/2 & \epsilon_{yy} & \gamma_{yz}/2 \\ \gamma_{zx}/2 & \gamma_{zy}/2 & \epsilon_{zz} } \right] \]
The exclusion of rigid body rotations from the strain tensor leads to \(\gamma_{xy} = \gamma_{yx}\), \(\gamma_{xz} = \gamma_{zx}\), and \(\gamma_{yz} = \gamma_{zy}\). This also produces symmetric tensors.
\[ \boldsymbol{\epsilon} = \left[ \matrix{ \epsilon_{11} & \epsilon_{12} & \epsilon_{13} \\ \epsilon_{12} & \epsilon_{22} & \epsilon_{23} \\ \epsilon_{13} & \epsilon_{23} & \epsilon_{33} } \right] = \left[ \matrix{ \epsilon_{xx} & \epsilon_{xy} & \epsilon_{xz} \\ \epsilon_{xy} & \epsilon_{yy} & \epsilon_{yz} \\ \epsilon_{xz} & \epsilon_{yz} & \epsilon_{zz} } \right] = \left[ \matrix{ \epsilon_{xx} & \gamma_{xy}/2 & \gamma_{xz}/2 \\ \gamma_{xy}/2 & \epsilon_{yy} & \gamma_{yz}/2 \\ \gamma_{xz}/2 & \gamma_{yz}/2 & \epsilon_{zz} } \right] \]