Compare the invariants of the strain tensor below with those of its deviatoric counterpart to answer the question.
\[ {\bf E} = \left[ \matrix{ \;\;\;0.50 & \;\;\;0.30 & -0.10 \\ \;\;\;0.30 & -0.10 & \;\;\;0.20 \\ -0.10 & \;\;\;0.20 & -0.10 } \right] \]
\[ \begin{eqnarray} I_1 & = & 0.50 + (-0.10) + (-0.10) \\ \\ & = & 0.30 \\ \\ I_2 & = & (0.50)(-0.10) + (-0.10)(-0.10) + (-0.10)(0.50) - (0.30)^2 - (-0.10)^2 - (0.20)^2 \\ \\ & = & -0.23 \\ \\ I_3 & = & \text{det}({\bf E}) \\ \\ & = & -0.017 \end{eqnarray} \]
The hydrostatic strain is one-third of \(I_1\): \(\epsilon_{Hyd} = 0.10\). Sutracting this from each diagonal component give the deviatoric strain tensor.
\[ {\bf E}' = \left[ \matrix{ \;\;\;0.40 & \;\;\;0.30 & -0.10 \\ \;\;\;0.30 & -0.20 & \;\;\;0.20 \\ -0.10 & \;\;\;0.20 & -0.20 } \right] \]
And the invariants of the deviatoric strain tensor are
\[ \begin{eqnarray} I_1 & = & 0.40 + (-0.20) + (-0.20) \\ \\ & = & 0.00 \\ \\ I_2 & = & (0.40)(-0.20) + (-0.20)(-0.20) + (-0.20)(0.40) - (0.30)^2 - (-0.10)^2 - (0.20)^2 \\ \\ & = & -0.26 \\ \\ I_3 & = & \text{det}({\bf E}') \\ \\ & = & 0.008 \end{eqnarray} \]
So the invariants of the (total) strain tensor and the deviatoric strain tensor are indeed different.
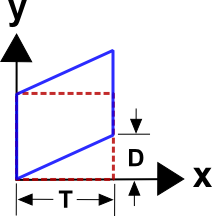
The mapping equations for this case are
\[ \begin{eqnarray} x & = & X \\ y & = & Y + X \left( {C \over T} \right) t \end{eqnarray} \]
The deformation gradient is
\[ {\bf F} = \left[ \matrix{ 1 & 0 \\ \\ \left( {C \over T} \right) t & 1 } \right] \]
Its inverse is
\[ {\bf F}^{-1} = \left[ \matrix{ 1 & 0 \\ \\ -\left( {C \over T} \right) t & 1 } \right] \]
And \(\dot {\bf F}\) is
\[ \dot {\bf F} = \left[ \matrix{ 0 & 0 \\ \\ \left( {C \over T} \right) & 0 } \right] \]
So \({\bf L}\) is
\[ \begin{eqnarray} {\bf L} = \dot {\bf F} \cdot {\bf F}^{-1} & = & \left[ \matrix{ 0 & 0 \\ \\ \left( {C \over T} \right) & 0 } \right] \left[ \matrix{ 1 & 0 \\ \\ -\left( {C \over T} \right) t & 1 } \right] \\ \\ \\ & = & \left[ \matrix{ 0 & 0 \\ \\ \left( {C \over T} \right) & 0 } \right] \end{eqnarray} \]
So in this rare example, \({\bf L} = \dot {\bf F}\).