Homework #3
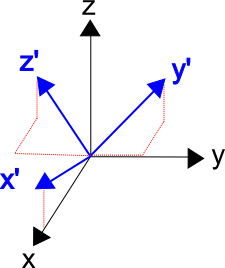
The coordinate system in the figure below has been transformed so that
all three axes form equal angles with the original \(z\)-axis, and the new
\(x'\)-axis is directly above the original \(x\)-axis.
Note - this orientation corresponds to the orientation of many
atomic crystals in face centered cubic (FCC) metals undergoing
tension in the Z-direction. Common FCC metals are aluminum, copper,
nickel, and steels at very high temperatures. Steel at room temperature
is body centered cubic (BCC).
-
What set of Roe angles will produce this transformation?
-
What single rotation axis and angle will produce the transformation?
-
A 2-D problem:
Given \( \quad {\bf v} = (5,9) \) and
\(\quad {\bf A} = \left[
\matrix {
5 & 2 \\
2 & 3
} \right] \quad
\),
apply a 180° coordinate rotation to both and show that the signs
of all the components change on one but not the other. Any insight
on this?
-
Show that
\(
\nabla \cdot \nabla || {\bf x} || = 2 / || {\bf x} ||
\)
