Homework #9
Reminder - you're going to need these webpages:
http://www.continuummechanics.org/techforms/index.html
to do this homework.... unless you prefer to use Matlab, Mathematica, etc.
-
We know that the 1st invariant of a deviatoric strain tensor is
automatically zero regardless of the 1st invariant's value for
the total strain tensor. But do the 2nd and 3rd invariants change
between the total strain and the deviatoric strain tensors?
Compare the invariants of the strain tensor below with those of its
deviatoric counterpart to answer the question.
\[
{\bf E} =
\left[ \matrix{
\;\;\;0.50 & \;\;\;0.30 & -0.10 \\
\;\;\;0.30 & -0.10 & \;\;\;0.20 \\
-0.10 & \;\;\;0.20 & -0.10
} \right]
\]
-
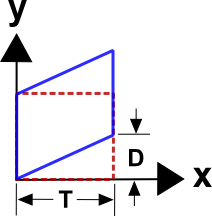
If an object is sheared, \((D/T)\) style, where \(D = C\,t\) and \(C\)
is a constant, then figure out the velocity gradient, \({\bf L}\), for this.
THAT'S All.
