Introduction
- If it's a physical quantity, like stress, then it's usually called a tensor. If it's not a physical quantity, then it's usually called a matrix.
- The vast majority of engineering tensors are symmetric. One common quantity that is not symmetric, and not referred to as a tensor, is a rotation matrix.
- Tensors are in fact any physical quantity that can be represented by a scalar, vector, or matrix. Zero-order tensors, like mass, are called scalars, while 1st order tensors are called vectors. Examples of higher order tensors include stress, strain, and stiffness tensors.
- The order, or rank, of a matrix or tensor is the number of subscripts it contains. A vector is a 1st rank tensor. A 3x3 stress tensor is 2nd rank.
- Coordinate Transformations of tensors are discussed in detail here.
Identity Matrix
\[ {\bf I} = \left[ \matrix{ 1&0&0 \\ 0&1&0 \\ 0&0&1 } \right] \]
Multiplying anything by the identity matrix is like multiplying by one.
Tensor Notation
The identity matrix in tensor notation is simply \( \delta_{ij} \). It is the Kronecker Delta that equals 1 when \( i = j \) and 0 otherwise.Is It a Matrix or Not?
A note from the purists... The identity matrix is a matrix, but the Kronecker delta technically is not. \( \delta_{ij} \) is a single scalar value that is either 1 or 0 depending on the values of \(i\) and \(j\). This is also why tensor notation is not in bold, because it always refers to individual components of tensors, but never to a tensor as a whole.Follow this link for an entertaining discussion between someone who gets it, and someone else who doesn't.
Kronecker Delta verses Dirac Delta
Don't confuse the Kronecker delta, \(\delta_{ij}\), with the Dirac delta, \(\delta_{(t)}\). The Dirac delta is something totally different. It is often used in signal processing and equals 0 for all \(t\) except \(t=0\). At \(t=0\), it approaches \(\infty\) such that\[ \int_{-\infty}^{\infty} f(t) \delta_{(t)} dt = f(0) \]
Transpose
The transpose of a matrix mirrors its components about the main diagonal. The transpose of matrix \({\bf A}\) is written \({\bf A}^{\!T}\).Transpose Example
\[ \text{If}\qquad{\bf A} = \left[ \matrix{ 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 } \right] ,\qquad\text{then}\qquad {\bf A}^{\!T} = \left[ \matrix{ 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 } \right] \]Tensor Notation
The transpose of \(A_{ij}\) is \(A_{j\,i}\).Determinants
\[ \begin{eqnarray} | {\bf A} | & = & \left| \matrix { A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} } \right| \\ \\ & = & A_{11} ( A_{22} A_{33} - A_{23} A_{32} ) + \\ & & A_{12} ( A_{23} A_{31} - A_{21} A_{33} ) + \\ & & A_{13} ( A_{21} A_{32} - A_{22} A_{31} ) \end{eqnarray} \]
If the determinant of a tensor, or matrix, is zero, then it does not have an inverse.
Tensor Notation
The calculation of a determinant can be written in tensor notation in a couple different ways\[ \text{det}( {\bf A} ) \; = \; \epsilon_{ijk} A_{i1} A_{j2} A_{k3} \; = \; {1 \over 6} \epsilon_{ijk} \epsilon_{rst} A_{ir} A_{js} A_{kt} \]
Determinant Example
If \( {\bf A} = \left[ \matrix { 3 & 2 & 1 \\ 5 & 7 & 4 \\ 9 & 6 & 8 } \right] \) , then its determinant is \[ \begin{eqnarray} | {\bf A} | & = & 3 * (7 * 8 - 4 * 6 ) + 2 * (4 * 9 - 5 * 8) + 1 * (5 * 6 - 7 * 9) \\ & & \\ & = & 3 * 32 + 2 * (-4) + 1 * (-33) \\ & & \\ & = & 96 - 8 - 33 \\ & & \\ & = & 55 \end{eqnarray} \]\[ \text{det}( {\bf A} \cdot {\bf B} ) = \text{det}( {\bf A} ) * \text{det}( {\bf B} ) \]
The determinant of a deformation gradient gives the ratio of initial to final volume of a differential element.
Inverses
The inverse of matrix \({\bf A}\) is written as \({\bf A}^{\!-1}\) and has the following very important property (see the section on matrix multiplication below)\[ {\bf A} \cdot {\bf A}^{\!-1} = {\bf A}^{\!-1} \cdot {\bf A} = {\bf I} \]
If \({\bf B}\) is the inverse of \({\bf A}\), then
\[ \begin{eqnarray} B_{11} & = & (A_{22} A_{33} - A_{23} A_{32} ) \; / \; \text{det}({\bf A}) \\ B_{12} & = & (A_{13} A_{32} - A_{12} A_{33} ) \; / \; \text{det}({\bf A}) \\ B_{13} & = & (A_{12} A_{23} - A_{13} A_{22} ) \; / \; \text{det}({\bf A}) \\ B_{21} & = & (A_{23} A_{31} - A_{21} A_{33} ) \; / \; \text{det}({\bf A}) \\ B_{22} & = & (A_{11} A_{33} - A_{13} A_{31} ) \; / \; \text{det}({\bf A}) \\ B_{23} & = & (A_{13} A_{21} - A_{11} A_{23} ) \; / \; \text{det}({\bf A}) \\ B_{31} & = & (A_{21} A_{32} - A_{22} A_{31} ) \; / \; \text{det}({\bf A}) \\ B_{32} & = & (A_{12} A_{31} - A_{11} A_{32} ) \; / \; \text{det}({\bf A}) \\ B_{33} & = & (A_{11} A_{22} - A_{12} A_{21} ) \; / \; \text{det}({\bf A}) \\ \end{eqnarray} \]
Inverse Example
If \( \quad {\bf A} = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \quad \) then \( \quad {\bf A}^{\!-1} = \left[ \matrix { \;\;\;1 & \;\;\;0.5 & -1 \\ -6 & -1 & \;\;\;5 \\ \;\;\;4 & \;\;\;0.5 & -3 } \right] \quad \) because\[ \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \left[ \matrix { \;\;\;1 & \;\;\;0.5 & -1 \\ -6 & -1 & \;\;\;5 \\ \;\;\;4 & \;\;\;0.5 & -3 } \right] = \left[ \matrix { \;\;\;1 & \;\;\;0.5 & -1 \\ -6 & -1 & \;\;\;5 \\ \;\;\;4 & \;\;\;0.5 & -3 } \right] \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] = \left[ \matrix { 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 } \right] \]
Tensor Notation
The inverse of \(A_{ij}\) is often written as \(A^{-1}_{ij}\). Note that this is probably not rigorously correct since, as discussed earlier, neither \(A_{ij}\) nor \(A^{-1}_{ij}\) are technically matrices themselves. They are only components of a matrix. Oh well...The inverse can be calculated using
\[ A^{-1}_{ij} = {1 \over 2 \, \text{det} ({\bf A}) } \epsilon_{jmn} \, \epsilon_{ipq} A_{mp} A_{nq} \]
Matrix Inverse Webpage
This page calculates the inverse of a 3x3 matrix.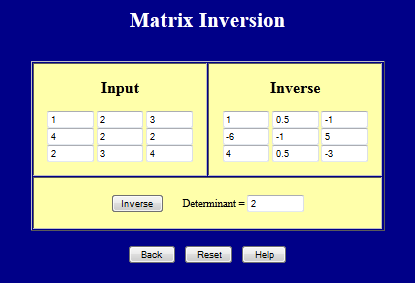
Transposes of Inverses of Transposes of...
The inverse of a transpose of a matrix equals the transpose of an inverse of the matrix. Since the order doesn't matter, the double operation is abbreviated simply as \({\bf{A}}^{\!-T}\).\[ {\bf{A}}^{\!-T} = \left( {\bf{A}}^{\!-1} \right)^{\!T} = \left( {\bf{A}}^T \right)^{\!-1} \]
Transpose / Inverse Example
If \( {\bf A} = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \), then\[ \left( {\bf{A}}^{\!-1} \right)^{T} : \qquad \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \qquad \overrightarrow{\text{Inverse}} \qquad \left[ \matrix { \;\;\; 1 & \;\;\;\; 0.5 & -1 \\ -6 & -1 & \;\; 5 \\ \;\; 4 & \;\;\;\; 0.5 & -3 } \right] \qquad \overrightarrow{\text{Transpose}} \qquad \left[ \matrix { \;\;\;\; 1 & -6 & \;\;\;\; 4 \\ \;\;\;\; 0.5 & -1 & \;\;\;\; 0.5 \\ \;-1 & \;\;\; 5 & \;-3 } \right] \]
\[ \left( {\bf{A}}^{T} \right)^{\!-1} : \qquad \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \qquad \overrightarrow{\text{Transpose}} \qquad \qquad \left[ \matrix { 1 & 4 & 2 \\ 2 & 2 & 3 \\ 3 & 2 & 4 } \right] \qquad \qquad \overrightarrow{\text{Inverse}} \qquad \left[ \matrix { \;\;\;\; 1 & -6 & \;\;\;\; 4 \\ \;\;\;\; 0.5 & -1 & \;\;\;\; 0.5 \\ \;-1 & \;\;\; 5 & \;-3 } \right] \]
So \(\left( {\bf{A}}^{\!-1} \right)^T\) does indeed equal \(\left( {\bf{A}}^T \right)^{\!-1}\).
Matrix Addition
Matrices and tensors are added component by component just like vectors. This is easily expressed in tensor notation.\[ C_{ij} = A_{ij} + B_{ij} \]
Matrix Multiplication (Dot Products)
\[ C_{ij} = A_{ik} B_{kj} \]
(Note that no dot is used in tensor notation.) The \(k\) in both factors automatically implies
\[ C_{ij} = A_{i1} B_{1j} + A_{i2} B_{2j} + A_{i3} B_{3j} \]
which is the ith row of the first matrix multiplied by the jth column of the second matrix. If, for example, you want to compute \(C_{23}\), then \(i=2\) and \(j=3\), and
\[ C_{23} = A_{21} B_{13} + A_{22} B_{23} + A_{23} B_{33} \]
Dot Product Example
If \( \quad {\bf A} = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \quad \) and \( \quad {\bf B} = \left[ \matrix { 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 } \right] \quad \) then \( \quad {\bf A} \cdot {\bf B} \) =\[ \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \left[ \matrix { 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 } \right] = \left[ \matrix { 14 & 32 & 50 \\ 14 & 38 & 62 \\ 20 & 47 & 74 } \right] \]
Matrix Multiplication Webpage
This page calculates the dot product of two 3x3 matrices.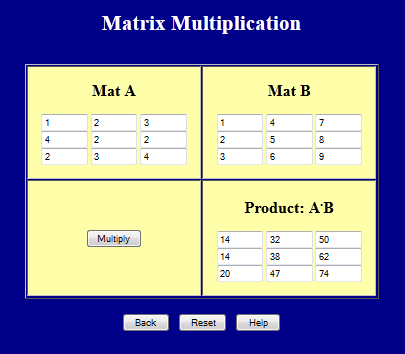
Tensor Notation and Computer Programming
Another advantage of tensor notation is that it spells out for you how to write the computer code to do it. Note how the subscripts in the FORTRAN example below exactly match the tensor notation for \(C_{ij} = A_{ik} B_{kj}\). This is true for all tensor notation operations, not just this matrix dot product.
subroutine aa_dot_bb(n,a,b,c)
dimension a(n,n), b(n,n), c(n,n)
do i = 1,n
do j = 1,n
c(i,j) = 0
do k = 1,n
c(i,j) = c(i,j) + a(i,k) * b(k,j)
end do
end do
end do
return
end
Matrix Multiplication Is Not Commutative
It is very important to recognize that matrix multiplication is NOT commutative, i.e.\[ {\bf A} \cdot {\bf B} \ne {\bf B} \cdot {\bf A} \]
Non-Commutativity Example
If \( \quad {\bf A} = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \quad \) and \( \quad {\bf B} = \left[ \matrix { 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 } \right] \quad \)\[ \text{then } {\bf A} \cdot {\bf B} = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \left[ \matrix { 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 } \right] = \left[ \matrix { 14 & 32 & 50 \\ 14 & 38 & 62 \\ 20 & 47 & 74 } \right] \]
\[ \text{but } \; {\bf B} \cdot {\bf A} = \left[ \matrix { 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 } \right] \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] = \left[ \matrix { 31 & 31 & 39 \\ 38 & 38 & 48 \\ 45 & 45 & 57 } \right] \]
So it is clear that \({\bf A} \cdot {\bf B}\) is not equal to \({\bf B} \cdot {\bf A}\).
Transposes and Inverses of Products
The transpose of a product equals the product of the transposes in reverse order, and the inverse of a product equals the product of the inverses in reverse order.Note that the "in reverse order" is critical. This is used extensively in the sections on deformation gradients and Green strains.
\[ ( {\bf A} \cdot {\bf B} )^T = {\bf B}^T \cdot {\bf A}^T \qquad \text{and} \qquad ( {\bf A} \cdot {\bf B} )^{-1} = {\bf B}^{-1} \cdot {\bf A}^{-1} \]
This also applies to multiple products. For example
\[ ( {\bf A} \cdot {\bf B} \cdot {\bf C} )^T = {\bf C}^T \cdot {\bf B}^T \cdot {\bf A}^T \]
Transpose of Products Example
then \( {\bf A} \cdot {\bf B} = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \left[ \matrix { 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 } \right] = \left[ \matrix { 14 & 32 & 50 \\ 14 & 38 & 62 \\ 20 & 47 & 74 } \right] \)
and \( ( {\bf A} \cdot {\bf B} )^T = \left[ \matrix { 14 & 14 & 20 \\ 32 & 38 & 47 \\ 50 & 62 & 74 } \right] \)
For comparison, \( {\bf B}^T \cdot {\bf A}^T = \left[ \matrix { 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 } \right] \left[ \matrix { 1 & 4 & 2 \\ 2 & 2 & 3 \\ 3 & 2 & 4 } \right] = \left[ \matrix { 14 & 14 & 20 \\ 32 & 38 & 47 \\ 50 & 62 & 74 } \right] \)
Product With Own Transpose
The product of a matrix and its own transpose is always a symmetric matrix. \( {\bf A}^T \cdot {\bf A} \) and \( {\bf A} \cdot {\bf A}^T \) both give symmetric, although different results. This is used extensively in the sections on deformation gradients and Green strains.Symmetric Product Example
If \( \quad {\bf A} = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \quad \)then \( {\bf A} \cdot {\bf A}^T = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \left[ \matrix { 1 & 4 & 2 \\ 2 & 2 & 3 \\ 3 & 2 & 4 } \right] = \left[ \matrix { 14 & 14 & 20 \\ 14 & 24 & 22 \\ 20 & 22 & 29 } \right] \)
and \( {\bf A}^T \cdot {\bf A} = \left[ \matrix { 1 & 4 & 2 \\ 2 & 2 & 3 \\ 3 & 2 & 4 } \right] \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] = \left[ \matrix { 21 & 16 & 19 \\ 16 & 17 & 22 \\ 19 & 22 & 29 } \right] \)
Both results are indeed symmetric, although they are unrelated to each other.
Double Dot Products
The double dot product of two matrices produces a scalar result. It is written in matrix notation as \({\bf A} : {\bf B}\). Although rarely used outside of continuum mechanics, is in fact quite common in advanced applications of linear elasticity. For example, \( {1 \over 2} \sigma : \epsilon \) gives the strain energy density in small scale linear elasticity. Once again, its calculation is best explained with tensor notation.\[ {\bf A} : {\bf B} = A_{ij} B_{ij} \]
Since the \(i\) and \(j\) subscripts appear in both factors, they are both summed to give
\[ \matrix { {\bf A} : {\bf B} \; = \; A_{ij} B_{ij} \; = & A_{11} * B_{11} & + & A_{12} * B_{12} & + & A_{13} * B_{13} & + \\ & A_{21} * B_{21} & + & A_{22} * B_{22} & + & A_{23} * B_{23} & + \\ & A_{31} * B_{31} & + & A_{32} * B_{32} & + & A_{33} * B_{33} & } \]
Double Dot Product Example
If \( \quad {\bf A} = \left[ \matrix { 1 & 2 & 3 \\ 4 & 2 & 2 \\ 2 & 3 & 4 } \right] \quad \) and \( \quad {\bf B} = \left[ \matrix { 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 } \right] \quad \) then\[ \matrix { {\bf A} : {\bf B}\; & = & 1 * 1 & + & 2 * 4 & + & 3 * 7 & + \\ & & 4 * 2 & + & 2 * 5 & + & 2 * 8 & + \\ & & 2 * 3 & + & 3 * 6 & + & 4 * 9 \\ & \\ & = & 124 } \]