Description
Fracture Mechanics Website
Thank You
Thank you for visiting this website. Feel free to email me if you have questions or comments.Also, please consider visiting an advertiser here. Doing so helps to cover website hosting fees.
Bob McGinty
bmcginty@gmail.com
PDFs of Entire Website - $12.95
For $12.95, you receive two formatted PDFs (the first for 8.5" x 11" pages, the second for tablets) of the entire website.Click here to see a sample page in each of the two formats.
| Email address to receive PDFs |
| Author | Bob McGinty, PhD, PE(ret) | |
| bmcginty@gmail.com |
Table of Contents
- INTRODUCTION
- BASIC MATHEMATICS
- Vectors
- Matrices & Tensors
- Vector Calculus
- Tensor Notation (Basic)
- Tensor Notation (Advanced)
- Coordinate Transformations
- Transformation Matrices
- Divergence Theorem
- Cylindrical Coordinates
- INTRODUCTORY MECHANICS
- DEFORMATIONS AND STRAIN
- Deformation Gradients
- Polar Decompositions
- Rotation Matrices
- Finite Element Mapping
- Small Scale Strains
- Green & Almansi Strains
- Principal Strains & Invariants
- Hydrostatic & Deviatoric Strains
- Velocity Gradients
- True Strain
- Material Derivative
- Special Strain Topics
- STRESS
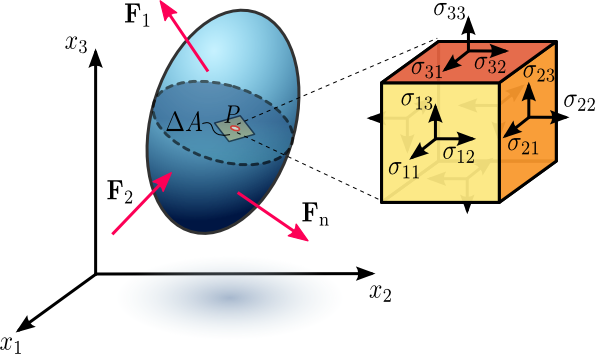
- Stress Introduction
- Traction Vectors
- Energetic Conjugates
- Stress Transformations
- Principal Stresses & Invariants
- Hydrostatic & Deviatoric Stresses
- Von Mises Stress
- Corotational Derivatives
- Equilibrium
- MATERIAL BEHAVIOR
- Continuity Equation
- Navier Stokes Equation
- Thermodynamics
- Hooke's Law
- Metal Plasticity
- Mooney-Rivlin Models
- Dynamic Material Properties
- Materials and Tire Behavior
- COLUMN BUCKLING
- SIGNAL PROCESSING
- MISCELLANEOUS TOPICS
- Strain Gauges
- Fasteners (in development)
External Links
- https://mechanicalc.com/
- http://www.thefullwiki.org/Continuum_mechanics
- http://en.wikipedia.org/wiki/Continuum_mechanics
- http://en.wikipedia.org/wiki/Finite_strain_theory
Fracture Mechanics Website
Visit my sister website, www.fracturemechanics.org, for information on fracture mechanics. It is under development, but will eventually contain information on linear and nonlinear fracture mechanics, as well as fatigue crack growth.A Note About The Web Technologies Used Here
Two relatively new web technologies are used on these pages. The first is Scalable Vector Graphics, or SVG. Pages on this site will display SVG files in compatible browsers, and PNG files in incompatible ones. The advantage of SVG over PNG is that SVG graphics can be scaled to any size without the onset of pixelization. SVG files used here were created using Inkscape, an excellent graphics program available free on the internet here.The second new technology used here is MathJax, a Javascript based display engine for mathematical equations programmed in the LaTeX language. MathJax eliminates the need to display equations as GIF or PNG graphics files (or even SVG for that matter). MathJax requires only the following line of code in the <HEAD> segment of a webpage.
<script type="text/javascript" src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.5/latest.js?config=TeX-MML-AM_CHTML"></script>
It is then possible to program any math expression in the HTML source using the LaTeX language. For example, typing
\(\sigma_{ij}\) produces \( \sigma_{ij} \).
I'm often asked what software I used to develop the webpages. The answer is... the Vim editor (www.vim.org). Vim is the Windows-based version of the venerable Vi editor on Unix, and now Linux systems. I typed everything by hand.
Bob McGinty
February 2012